Eine Kapitalmehrung kannst du dir so vorstellen, dass auf deinem Konto bereits ein Startkapital/Anfangskapital liegt. Nun bezahlst du zusätzlich regelmäßigen Abständen am Anfang oder am Ende eines Jahres einen gleichbleibenden Betrag (r) ein. Das Kapital auf deinem Konto mehr sich dementsprechend.
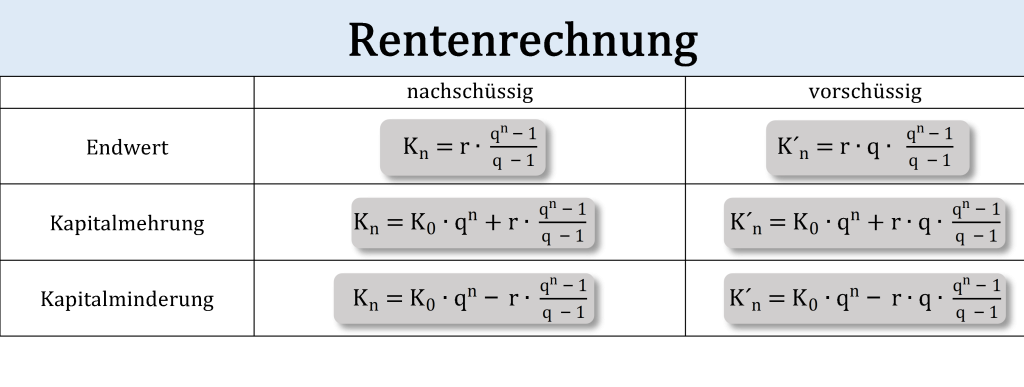
Bei der Kapitalmehrung kombinieren wir die Zineszinsrechnung mit der vor- bzw. nachschüssigen Rentenrechnung. Man nennt diesen Teilbereich der Finanzmathematik deshalb auch kombinierte Zineszins-/Rentenrechnung.
Die Formel für die Zinseszinsen lautet:
K_{n} = K_{0}*q^nDie Formel für den Endwert einer nachschüssigen Rentenrechnung lautet:
K_{n}=r*\frac{q^n-1}{q-1}Die nachschüssige kombinierte Zinseszins-/Rentenrechnung einer Kapitalmehrung setzt nun beide Rechnungen „zusammen“:
K_{n}=K_{0}*q^n+r*\frac{q^n-1}{q-1}Beispielaufgabe: Auf deinem Konto befindet sich bereits ein Startkapital von 10.000,00 €. Du legst nun, immer am Ende eines Jahres, die gleichbleibende Sparrate in Höhe von 2.000,00 € an. Welchen Betrag hast du nach 8 Jahren auf deinem Konto, wenn dir deine Bank 2,3% Zinsen p.a. bietet? Informiere dich selbstständig im Lernvideo und löse anschließend schriftlich. Viel Erfolg 🙂
Wir haben folgende Angaben gegeben:
K_{0} = 10.000\ |\ q=1+\frac{2,3}{100}=1,023\ |\ r=2.000\ |\ n=8Gesucht ist das Endkapital nach 8 Jahren einer nachschüssigen Kapitalmehrung:
K_{n}=K_{0}*q^n+r*\frac{q^n-1}{q-1}=10.000*1,023^8+2.000*\frac{1,023^8-1}{1,023-1}=29.344,12\ €Nach 8 Jahren hättest du 29.344,12 € auf deinem Konto.
Berechnung der Sparrate „r“
Bei der Kapitalmehrung gibt es Aufgabentypen, in denen nicht das Endkapital, sondern die jährliche Sparrate „r“ gesucht ist.
Beispielaufgabe 2: Sabine hat bereits 15.000,00 € auf ihrem Konto. Welchen jährlich gleichbleibenden Betrag muss sie am Ende eines jeden Jahres anlegen, um nach 5 Jahren 40.000,00 € auf ihrem Konto zu haben, wenn das Kapital mit 3,3 % Zinsen p.a. verzinst wird. Informiere dich im Lernvideo ab Minute 3:50. viel Erfolg!