Trigonometrie

Die Trigonometrie (vom griechischen „trigonon – Dreieck“) ist ein Teilgebiet der Geometrie, bei der Verhältnisse von Seiten und Winkeln in Dreiecken untersucht werden. Du kannst hier lernen, wie man mit Hilfe von Sinus (sin), Kosinus (cos) und Tangens (tan) Streckenlängen und Winkel bestimmt.

Wir unterscheiden hier zwischen der Trigonometrie in rechtwinkligen und in allgemeinen Dreiecken.

Hier gehts zur vollständigen Playlist Trigonometrie auf YouTube

Trigonometrie in rechtwinkligen Dreiecken

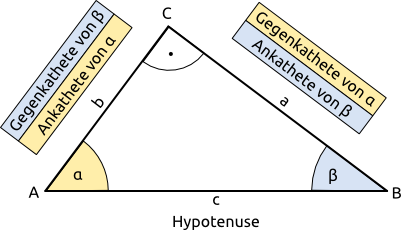
Was sind Ankathete und Gegenkathete? Ein rechtwinkliges Dreieck korrekt beschriften.

Fehlende Seite in einem rechtwinkligen Dreieck berechen (Sinus, Kosinus, Tangens)

Winkel berechnen bei 2 gegebenen Seiten

Übungsaufgaben

Bei einem rechtwinkligen Dreieck sind die Ankathete 14 cm und die Hypotenuse 17 cm lang. Berechne den eingeschlossenen Winkel.
In einem Dreieck beträgt die Ankathete 4 cm und der Winkel zwischen Ankathete und Hypotenuse ist 60°. Wie lang ist die Hypotenuse?
In einem Dreieck beträgt die Gegenkathete 5 cm und der Winkel zwischen Gegenkathete und Hypotenuse ist 30°. Wie lang ist die Hypotenuse?
In einem Dreieck beträgt die Hypotenuse 6 cm und der Winkel zwischen Hypotenuse und Gegenkathete ist 45°. Wie lang ist die Gegenkathete?
Eine Leiter lehnt an einer Wand. Die untere Leitersprosse ist 1,5 m von der Wand entfernt. Die Leiter selbst ist 3 m lang. In welchem Winkel zur Wand ist die Leiter geneigt?
Ein Stück Papier hat die Form eines rechtwinkligen Dreiecks, bei dem die Hypotenuse 10 cm lang ist. Es wird so aufgestellt, dass die Hypotenuse horizontal liegt. Wie hoch ist das Dreieck an der höchsten Stelle, wenn die Ankathete 6 cm lang ist?

2 Seiten gegebene, Winkel gesucht. Winkel zwischen Ankathete und Hypotenuse
Lösung: Mit Kosinus
cos(x) = Ankathete / Hypotenuse = 14/17
cos^-1(14/17) = 34,56°
Winkel = 34,56°
Gesucht: Hypotenuse
Lösung: Mit Sinus:
sin(60°) = Gegenkathete / Hypotenuse
Hypotenuse = Gegenkathete / sin(60°)
Hypotenuse = 4 / 0,866 = 4,62 cm
Gesucht: Hypotenuse
Lösung: Mit Cosinus:
cos(30°) = Gegenkathete / Hypotenuse
Hypotenuse = Gegenkathete / cos(30°)
Hypotenuse = 5 / 0,866 = 5,77 cm
Gesucht: Gegenkathete
Lösung: Mit Sinus:
sin(45°) = Gegenkathete / Hypotenuse
Gegenkathete = Hypotenuse * sin(45°)
Gegenkathete = 6 * 0,707 = 4,24 cm
Gesucht: Neigungswinkel der Leiter
Lösung: Mit Tangens:
tan(x) = Höhe / Entfernung zur Wand
Höhe = Hypotenuse * sin(x)
tan(x) = Höhe / Entfernung zur Wand
tan(x) = Hypotenuse * sin(x) / Entfernung zur Wand
x = arctan(Hypotenuse * sin(x) / Entfernung zur Wand)
x = arctan(3 / 1,5) = 63,43°
Gesucht: Höhe des Dreiecks
Lösung: Mit Pythagoras:
Hypotenuse² = Ankathete² + Gegenkathete²
Gegenkathete = Höhe des Dreiecks
Hypotenuse = 10 cm, Ankathete = 6 cm
Höhe² = 10² – 6²
Höhe = sqrt(64) = 8 cm

Trigonometrie in allgemeinen Dreiecken

Der Sinussatz (Trigonometrie im allgemeinen Dreieck)

Der Kosinussatz (im allgemeinen Dreieck)

Der Flächensatz im allgemeinen Dreieck