Wenn du drei Punkte miteinander verbindest, die nicht auf einer Linie liegen, entsteht ein Dreieck 🙂 Logisch soweit! Wir unterteilen Dreiecke in drei wichtige Gruppen:
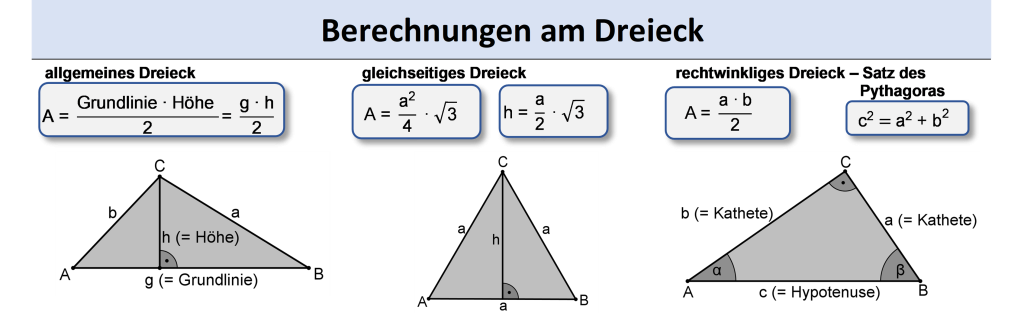
Das allgemeine Dreieck
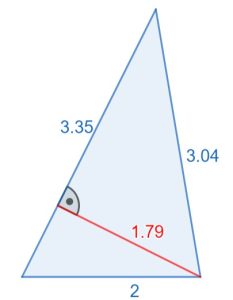
Jedes Dreieck ist ein allgemeines Dreieck. Die Höhe steht dabei senkrecht auf der Grundlinie. Theoretisch kann jede Seite eine Grundlinie sein, je nachdem wie du das Dreieck drehst.
Das gleichseitige Dreieck
Beim gleichseitigen Dreieck sind – Überraschung – alle 3 Seiten gleichlang.
Das rechtwinklige Dreieck
Beim rechtwinkligen Dreieck hat einer der drei Winkel 90°. In diesen Dreiecken kannst du zum Beispiel den Satz des Pythagoras oder Sinus, Kosinus und Tangens anwenden. Die längste Seite liegt gegenüber des rechten Winkels und heißt „Hypotenuse“. Die kurzen Seiten nennt man „Kathete“
Beispielaufgabe: Berechne den Flächeninhalt der nachfolgenden Dreiecke. Überlege zuerst. um welches Dreieck (allgemein, gleichseitig oder rechtwinklig) und halte deine Berechnungen schriftlich fest. Alle Einheiten sind in cm angegeben. Weiter unter findest du eine entsprechende Formelsammlung.
Dreieck A
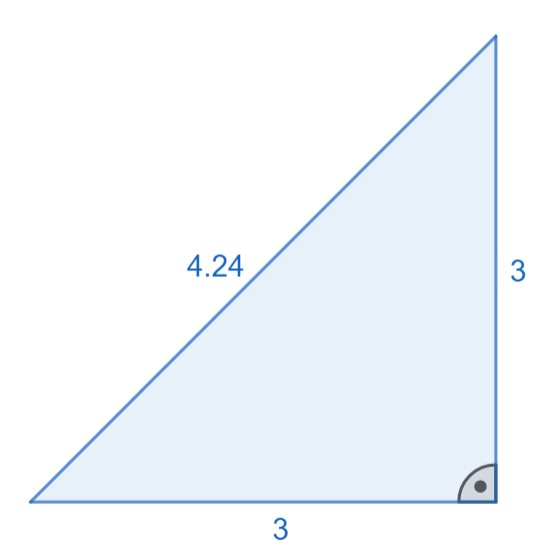
Dreieck B
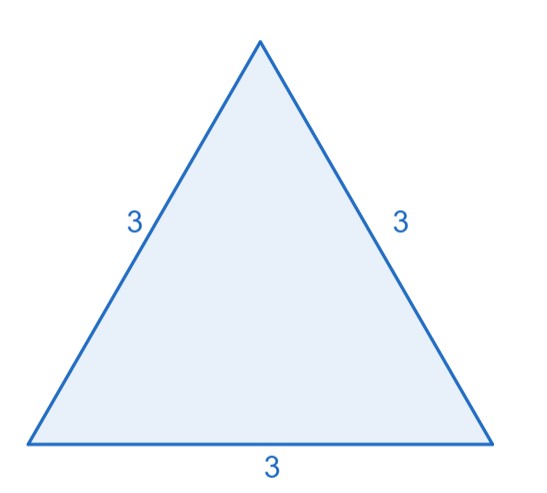
Dreieck C
Dreieck A ist ein rechtwinkliges Dreieck. Die Berechnung des Flächeninhalts kann so vorgenommen werden:
A = \frac{g*h}{2} =\frac{3*3}{2} = 4,5\ cm²Dreieck B ist ein gleichseitiges Dreieck mit der Streckenlänge a = 3. Berechnung:
A=\frac{a²}{4}*\sqrt{3}=\frac{3²}{4}*\sqrt{3}\approx3,90\ cm²Dreieck C ist ein allgemeines Dreieck. Die Höhe h = 1,79 und steht senkrecht auf der Grundseite g = 3,35. Berechnung:
A = \frac{g*h}{2} =\frac{3,35*1,79}{2} =2,99825\ cm²Beim Aufgabenfuchs findest du tolle Übungsaufgaben zur Berechnung an Dreiecken. Viel Spaß 🙂