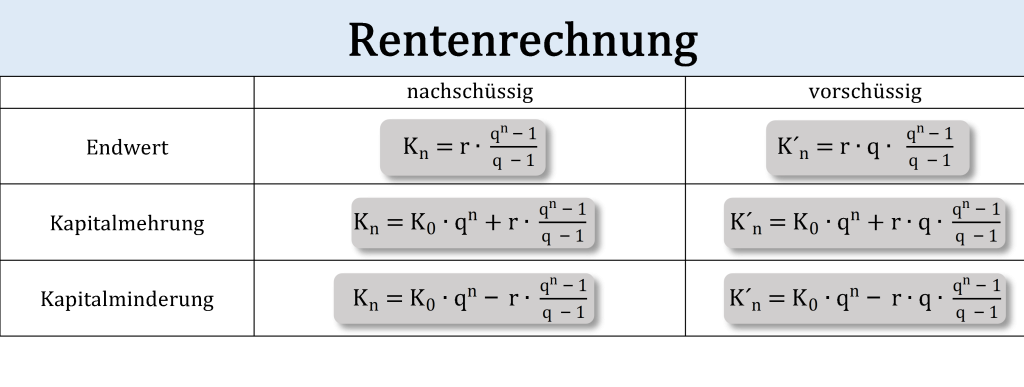
Bei einer Kapitalminderung lässt du dir in regelmäßigen Abständen (zu Beginn oder am Ende eines Jahres) eine gleichbleibende Rate ausbezahlen. Das Kapital, welches auf deinem Konto liegt, wird also immer weniger.
Auch hier kombinieren wir wieder die Zineszinsrechnung mit der Rentenrechnung. W
K_{n} = K_{0}*q^n\ und\ K_{n}=r*q*\frac{q^n-1}{q-1}Werden zur vorschüssigen kombinierte Zinseszins-/Rentenrechnung einer Kapitalminderung :
K_{n}=K_{0}*q^n-r*q*\frac{q^n-1}{q-1}Berechnung Endwert Kn Kapitalminderung
Beispielaufgabe Kapitalminderung: Du hast momentan 100.000,00 € auf deinem Konto und möchtest dir jeweils am Anfang eines jeden Jahres 5.000,00 € ausbezahlen lassen. Deine Bank bietet dir einen Zinssatz von 3 % p.a. . Wie viel Geld hast du nach 8 Jahre noch auf deinem Konto? Berechne!
K_{n}=K_{0}*q^n-r*q*\frac{q^n-1}{q-1} = 100.000 *1,03^8-5.000*1,03^8*\frac{1,03^8-1}{1,03-1} =70.354,28\ €Nach 8 Jahren wären noch 70.354,28 € auf deinem Konto.
Berechnung Laufzeit n bei einer Kapitalminderung
Nicht bei allen Aufgaben wird das Endkapital gesucht, häufig auch die Laufzeit „n“ oder die Sparrate „r“ (wird dir bei der Kapitalmehrung erklärt).
Beispielaufgabe Laufzeit „n“ gesucht: Herr Murx hat momentan 150.000,00 € auf seinem Konto. Er möchte wissen, wie häufig (also wie viele Jahre) er sich 10.000,00 € am Ende eines jeden Jahres ausbezahlen lassen könnten, bis er kein Geld mehr auf dem Konto hat. Seine Bank bietet ihm einen Zinssatz von 2 % p.a.
Schau dir das passende Lernvideo (Auflösen der Formel nach Laufzeit „n“) an und löse anschließend selbstständig. Viel Erfolg 🙂