Du kennst mit Sicherheit Pyramiden. Besonders bekannt sind die Pyramiden von Gizeh in Ägypten. Wir werden uns auf dieser Seite hauptsächlich mit Berechnungen an quadratischen Pyramiden beschäftigen.
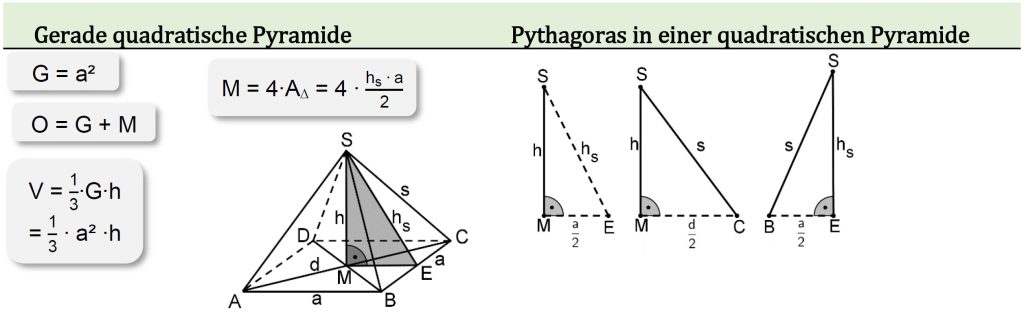
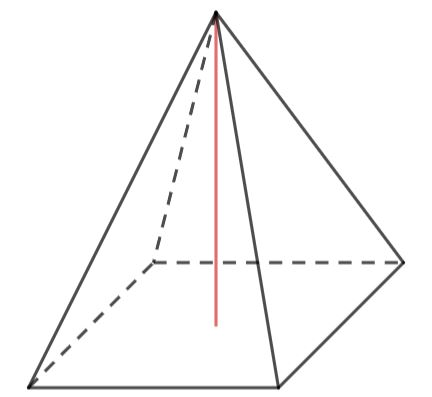
Quadratische Pyramide
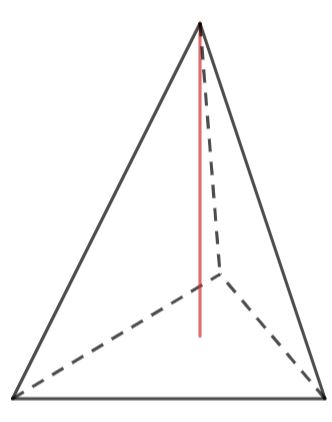
Dreieckspyramide
Beispielaufgabe: Berechne die Grundfläche, das Volumen und die Oberfläche einer quadratischen Pyramide, deren Seitenkante eine Länge von 5 cm hat und 8 cm hoch ist.
Die Seitenkante der quadratische Pyramide aus ist a = 5cm und die Höhe h = 8cm.
Die Grundfläche G ist ein Quadrat und kann daher durch G = 5cm*5cm = 25 cm² bestimmt werden.
Berechnung Volumen
V=\frac{1}{3}*G*h=\frac{1}{3}*(5cm*5cm)*8cm \approx66,67 cm³Berechnung Oberfläche
Die Oberfläche setzt sich aus der Grundfläche und der Mantelfläche zusammen. Die Grundfläche kennen wir bereits (25cm²), also berechnen wir die Mantelfläche M. Diese setzt sich bei einer quadratischen Pyramide aus 4 gleichgroßen Dreiecken zusammen.
M=4*A_{Dreieck}=4*\frac{h_{s}*a}{2}Um die Seitenlinie hs zu berechnen benötigen wir den Satz des Pythagoras.
h_{s}=\sqrt{h^2+(\frac{a}{2})^2}=\sqrt{8^2+(\frac{5}{2})^2}\approx8,38