Die meisten von euch kennen den Satz des Pythagoras bereits. Teste dein Wissen mit der Beispielaufgabe. Anschließend findest du weitere, digitale Übungsaufgaben.
Beispielaufgabe
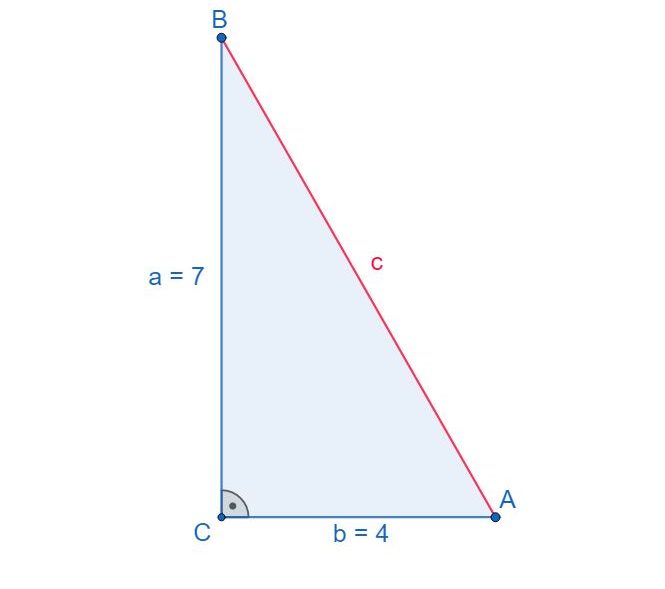
In einem rechtwinkligen Dreieck ABC, sind die Strecken a = 7 und b = 4 bekannt. Wir möchten rechnerisch die Länge der Strecke c bestimmen.
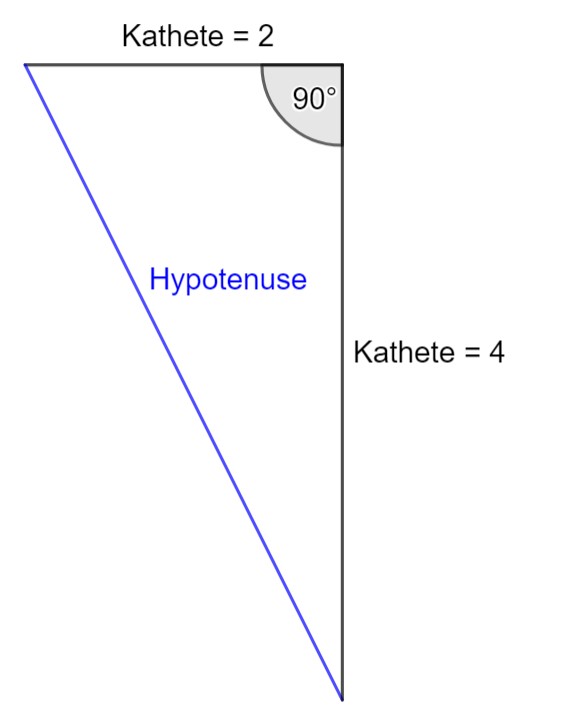
Überlege dir zunächst, wo sich im abgebildeten Dreieck die Katheten bzw. die Hypotenuse befindet.
Berechne anschließend mit Hilfe des Satz des Pythagoras die Streckenlänge „c“
Um den Satz des Pythagoras anwenden zu können, müssen wir uns zunächst über zwei Dinge Gedanken machen.
1. Handelt es sich um ein rechtwinkliges Dreieck?
2. Wo befindet sich die Hypotenuse bzw. die Katheten?
Der Satz des Pythagoras kann ausschließlich in einem rechtwinkligen Dreieck (das bedeutet, ein Winkel des Dreiecks hat 90°) angewandt werden. Die Hypotenuse ist die längste Strecke in einem rechtwinkligen Dreieck und befindet sich immer gegenüber des rechten Winkels.
Sind diese Bedingungen erfüllt, kann der Satz des Pythagoras angewandt werden.
Der Satz des Pythagoras lautet allgemein:
Kathete ² + Kathete ² = Hypotenuse ²
Beachte, dass die Katheten bzw. die Hypotenuse jeweils quadriert (hoch 2) genommen werden!
Häufig wird der Satz des Pythagoras auch mit
a² + b² = c²
dargestellt. Diese Formelschreibweise gilt aber nur in einem Dreieck, in dem die Hypotenuse mit „c“ abgekürzt wurde.
In der rechts abgebildeten Grafik sind die Katheten 2 bzw. 4 Längeneinheiten lang. Ich kann die Länge der Hypotenuse wie folgt berechnen:
Kathete ² + Kathete ² = Hypotenuse ²
2² + 4² = Hypotenuse²
4 + 16 = Hypotenuse²
20 = Hypotenuse² | Wurzel ziehen
Um die Streckenlänge der Hypotenuse zu erhalten muss nun noch die Wurzel gezogen werden. Das Ergebnis wurde auf 2 Stellen nach dem Komma gerundet.
\sqrt{20} = Hypotenuse \approx 4,47
Es handelt sich um ein rechtwinkliges Dreieck, mit den Katheten a = 7 und b = 4. Die Hypotenuse ist die Rote Strecke c.
Der Satz des Pythagoras lautet wie folgt:
Kathete²+Kathete² = Hypotenuse²
7² + 4² = c²
49 + 16 = c²
65 = c²
Jetzt muss noch die Wurzel aus 65 gezogen werden. Hierbei hilft der Taschenrechner.
c = \sqrt{65} \approx8,06Beim Aufgabenfuchs findest du passende Übungsaufgabe.