Die Trigonometrie (vom griechischen „trigonon – Dreieck“) ist ein Teilgebiet der Geometrie, bei der Verhältnisse von Seiten und Winkeln in Dreiecken untersucht werden. Du kannst hier lernen, wie man mit Hilfe von Sinus (sin), Kosinus (cos) und Tangens (tan) Streckenlängen und Winkel bestimmt.
Wir unterscheiden hier zwischen der Trigonometrie in rechtwinkligen und in allgemeinen Dreiecken.
Hier gehts zur vollständigen Playlist Trigonometrie auf YouTube
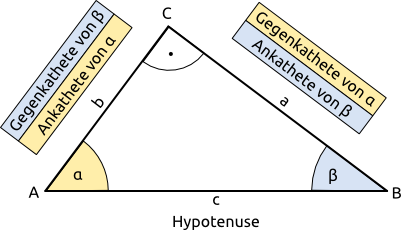
1. Trigonometrie in rechtwinkligen Dreiecken
Lernvideos
Übungsaufgaben
2. Trigonometrie in allgemeinen Dreiecken
10 Übungsaufgaben zur Trigonometrie mit Sinussatz
Berechne die gesuchten Größen in allgemeinen Dreiecken mit Hilfe des Sinussatzes. Runde deine Ergebnisse auf zwei Dezimalstellen.
Zur Erinnerung – der Sinussatz lautet: a/sin(α) = b/sin(β) = c/sin(γ)
In einem Dreieck sind die Seite a = 8 cm, der Winkel α = 42° und der Winkel β = 63° gegeben. Berechne die Länge der Seite b.
In einem Dreieck sind die Seite a = 15 cm, die Seite b = 12 cm und der Winkel α = 38° gegeben. Berechne den Winkel β.
In einem Dreieck sind die Seite b = 7 cm, der Winkel α = 45° und der Winkel β = 35° gegeben. Berechne die Länge der Seite a.
In einem Dreieck sind die Seite a = 10 cm, die Seite c = 12 cm und der Winkel α = 50° gegeben. Berechne den Winkel γ.
In einem Dreieck sind die Seite a = 18 cm, der Winkel β = 42° und der Winkel γ = 68° gegeben. Berechne die Länge der Seite c.
In einem Dreieck sind die Seite b = 14 cm, die Seite c = 20 cm und der Winkel β = 55° gegeben. Berechne den Winkel γ.
In einem Dreieck sind die Seite a = 12 cm, der Winkel α = 40° und der Winkel γ = 65° gegeben. Berechne die Länge der Seite c.
In einem Dreieck sind die Seite a = 25 cm, die Seite b = 18 cm und der Winkel β = 58° gegeben. Berechne den Winkel α.
In einem Dreieck sind die Seite c = 16 cm, der Winkel α = 45° und der Winkel β = 60° gegeben. Berechne die Länge der Seite a.
In einem Dreieck sind die Seite b = 22 cm, die Seite c = 18 cm und der Winkel β = 72° gegeben. Berechne den Winkel γ.
10 Übungsaufgaben zur Trigonometrie mit Kosinussatz
Berechne die gesuchten Größen in allgemeinen Dreiecken mit Hilfe des Kosinussatzes. Runde deine Ergebnisse auf zwei Dezimalstellen.
Zur Erinnerung - der Kosinussatz lautet:
- a² = b² + c² - 2·b·c·cos(α)
- b² = a² + c² - 2·a·c·cos(β)
- c² = a² + b² - 2·a·b·cos(γ)
Umgeformt für die Winkel:
- cos(α) = (b² + c² - a²) / (2·b·c)
- cos(β) = (a² + c² - b²) / (2·a·c)
- cos(γ) = (a² + b² - c²) / (2·a·b)
In einem Dreieck sind die Seiten a = 8 cm, b = 12 cm und c = 15 cm gegeben. Berechne den Winkel α.
Lösung:
Wir verwenden den Kosinussatz für den Winkel α:
cos(α) = (b² + c² - a²) / (2·b·c)
cos(α) = (12² + 15² - 8²) / (2·12·15)
cos(α) = (144 + 225 - 64) / 360
cos(α) = 305 / 360
cos(α) = 0,8472
α = arccos(0,8472) ≈ 32,20°
In einem Dreieck sind die Seiten a = 10 cm, c = 14 cm und der Winkel β = 60° gegeben. Berechne die Länge der Seite b.
Lösung:
Wir verwenden den Kosinussatz für die Seite b:
b² = a² + c² - 2·a·c·cos(β)
b² = 10² + 14² - 2·10·14·cos(60°)
b² = 100 + 196 - 2·10·14·0,5
b² = 296 - 140
b² = 148
b = √148 ≈ 12,17 cm
In einem Dreieck sind die Seiten b = 15 cm, c = 18 cm und der Winkel α = 45° gegeben. Berechne die Länge der Seite a.
Lösung:
Wir verwenden den Kosinussatz für die Seite a:
a² = b² + c² - 2·b·c·cos(α)
a² = 15² + 18² - 2·15·18·cos(45°)
a² = 225 + 324 - 2·15·18·0,7071
a² = 549 - 2·15·18·0,7071
a² = 549 - 381,834
a² = 146,66
a = √146,66 ≈ 12,11 cm
In einem Dreieck sind die Seiten a = 12 cm, b = 9 cm und c = 7 cm gegeben. Berechne den Winkel γ.
Lösung:
Wir verwenden den Kosinussatz für den Winkel γ:
cos(γ) = (a² + b² - c²) / (2·a·b)
cos(γ) = (12² + 9² - 7²) / (2·12·9)
cos(γ) = (144 + 81 - 49) / 216
cos(γ) = 176 / 216
cos(γ) = 0,8148
γ = arccos(0,8148) ≈ 35,60°
In einem Dreieck sind die Seiten a = 20 cm, c = 16 cm und der Winkel β = 50° gegeben. Berechne die Länge der Seite b.
Lösung:
Wir verwenden den Kosinussatz für die Seite b:
b² = a² + c² - 2·a·c·cos(β)
b² = 20² + 16² - 2·20·16·cos(50°)
b² = 400 + 256 - 2·20·16·0,6428
b² = 656 - 410,39
b² = 245,61
b = √245,61 ≈ 15,70 cm
In einem Dreieck sind die Seiten a = 18 cm, b = 14 cm und der Winkel γ = 65° gegeben. Berechne die Länge der Seite c.
Lösung:
Wir verwenden den Kosinussatz für die Seite c:
c² = a² + b² - 2·a·b·cos(γ)
c² = 18² + 14² - 2·18·14·cos(65°)
c² = 324 + 196 - 2·18·14·0,4226
c² = 520 - 2·18·14·0,4226
c² = 520 - 212,59
c² = 307,41
c = √307,41 ≈ 17,53 cm
Anmerkung: Die Toleranz beim Prüfen berücksichtigt verschiedene Rundungen in der Berechnung.
In einem Dreieck sind die Seiten b = 12 cm, c = 10 cm und der Winkel α = 70° gegeben. Berechne die Länge der Seite a.
Lösung:
Wir verwenden den Kosinussatz für die Seite a:
a² = b² + c² - 2·b·c·cos(α)
a² = 12² + 10² - 2·12·10·cos(70°)
a² = 144 + 100 - 2·12·10·0,342
a² = 244 - 82,08
a² = 161,92
a = √161,92 ≈ 12,73 cm
Anmerkung: Die Toleranz beim Prüfen berücksichtigt verschiedene Rundungen in der Berechnung.
In einem Dreieck sind die Seiten a = 22 cm, b = 16 cm und c = 14 cm gegeben. Berechne den Winkel β.
Lösung:
Wir verwenden den Kosinussatz für den Winkel β:
cos(β) = (a² + c² - b²) / (2·a·c)
cos(β) = (22² + 14² - 16²) / (2·22·14)
cos(β) = (484 + 196 - 256) / 616
cos(β) = 424 / 616
cos(β) = 0,6883
β = arccos(0,6883) ≈ 46,51°
Anmerkung: Die Toleranz beim Prüfen berücksichtigt verschiedene Rundungen in der Berechnung.
In einem Dreieck sind die Seiten a = 9 cm, b = 7 cm und der Winkel γ = 55° gegeben. Berechne die Länge der Seite c.
Lösung:
Wir verwenden den Kosinussatz für die Seite c:
c² = a² + b² - 2·a·b·cos(γ)
c² = 9² + 7² - 2·9·7·cos(55°)
c² = 81 + 49 - 2·9·7·0,5736
c² = 130 - 2·9·7·0,5736
c² = 130 - 72,27
c² = 57,73
c = √57,73 ≈ 7,60 cm
Anmerkung: Die Toleranz beim Prüfen berücksichtigt verschiedene Rundungen in der Berechnung.
