y = m*x

**Ursprungsgeraden der Form y = m*x**

Lineare Funktionen der Form y = m*x nennt man Ursprungsgeraden, weil sie durch den Ursprung des Koordinatensystems im Punkt (0|0) verlaufen.

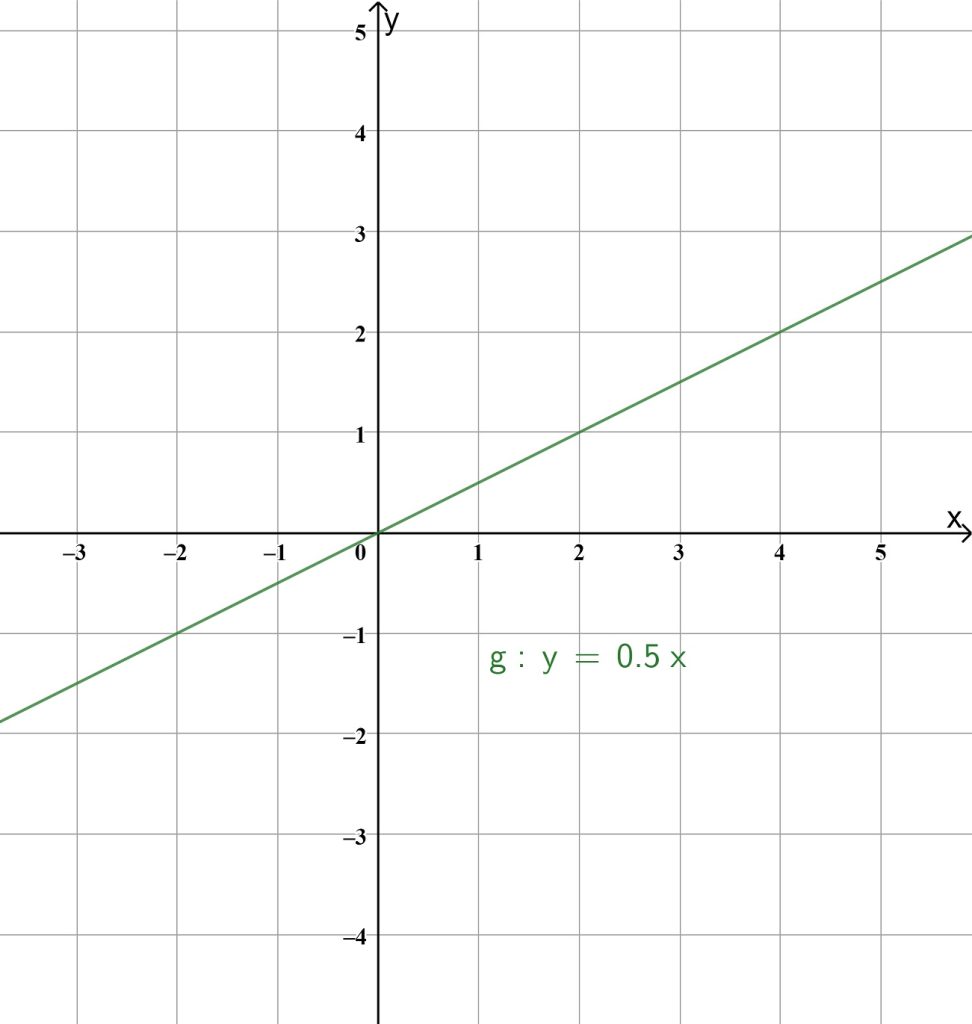
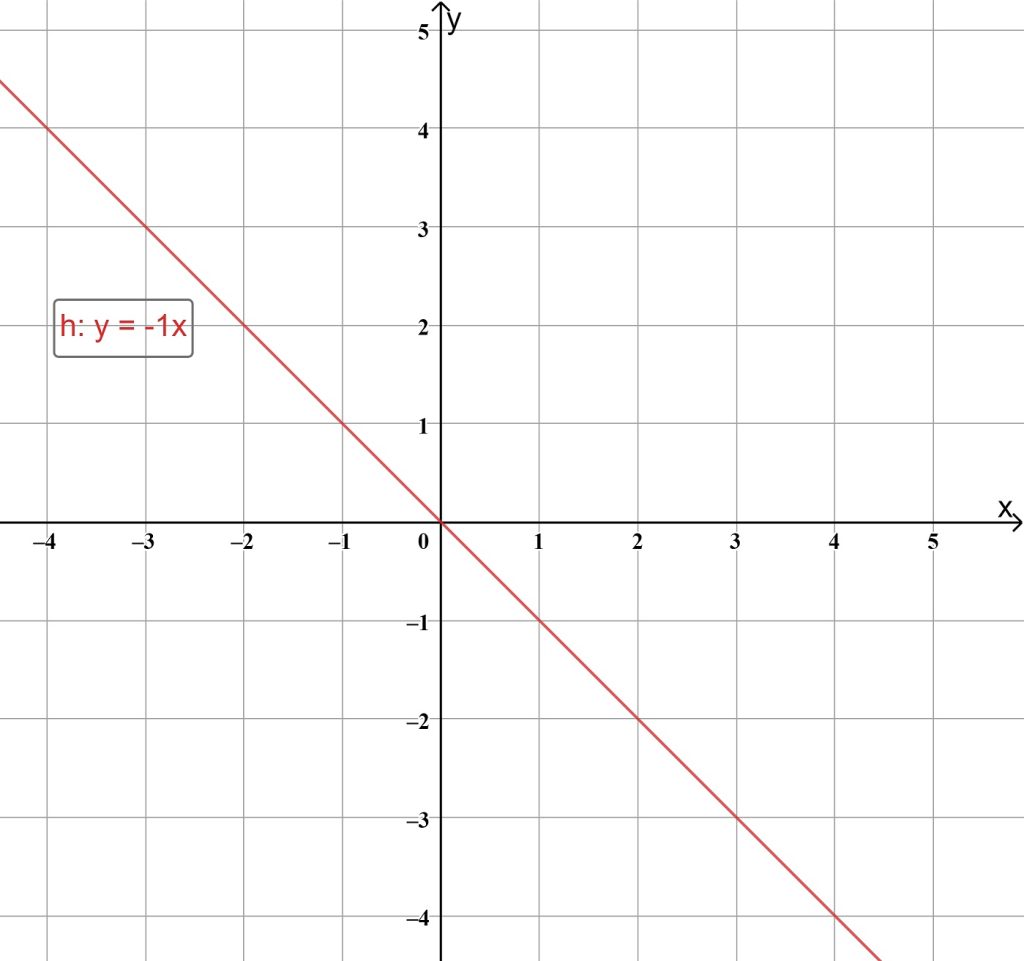
Beispiele für Ursprungsgeraden im Koordinatensystem:

y=2x

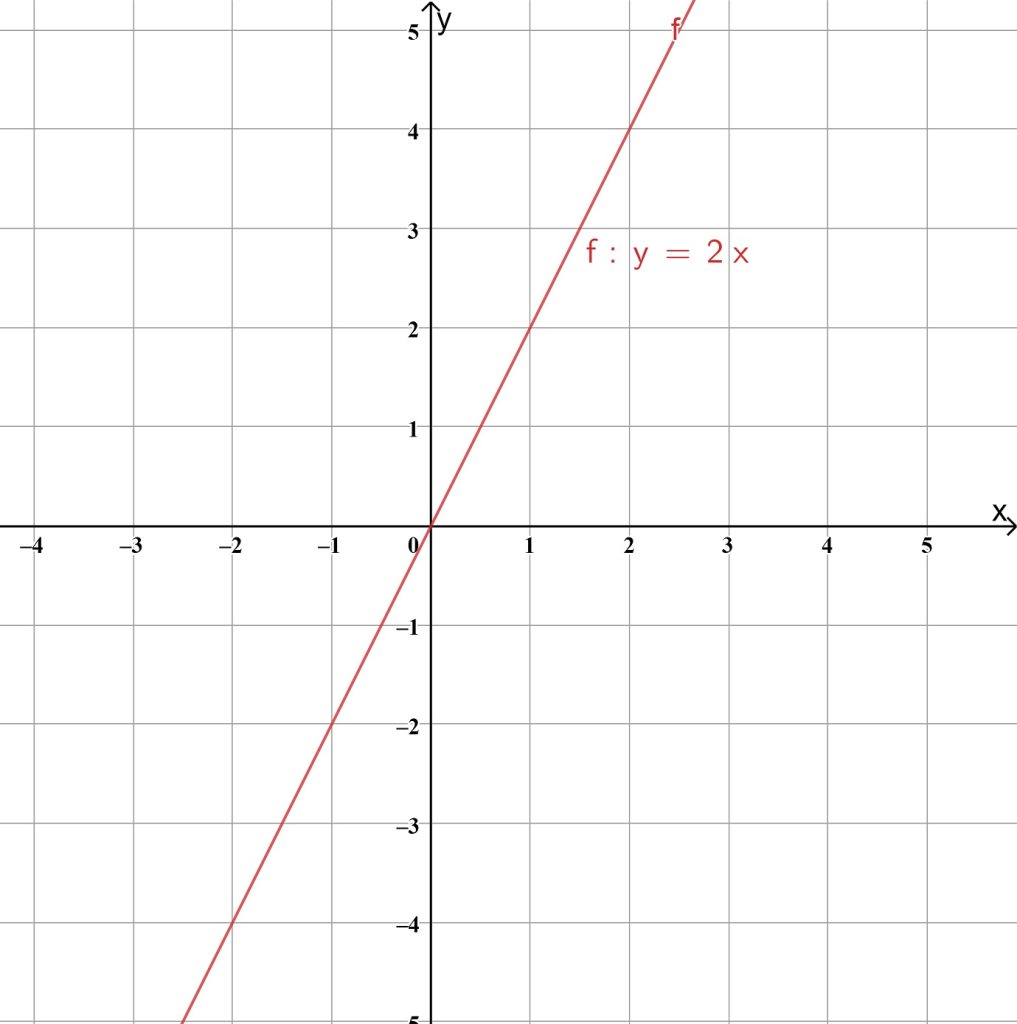
y=0.5x

y=-1x

Übungsaufgabe Ursprungsgeraden und Wertetabelle:

Erstelle für die Funktionsgleichungen y = x und y = 3x eine Wertetabelle (x von -4 bis 5) und zeichne anschließend die dazugehörigen Ursprungsgeraden bzw. Funktionsgraphen in ein Koordinatensystem (x und y-Achse von -5 bis 5). Du benötigst Hilfe? Im Lernvideo weiter unten wird dir alles erklärt 🙂

Im Lernvideo bis Minute 11:30 findest du eine Erklärung und Lösung.

Die Steigung m einer linearen Funktion

Neben der Gemeinsamkeit, dass alle Ursprungsgeraden durch denselben Punkt verlaufen, gibt es aber auch einen großen Unterschied. Die Funktionsgraphen verlaufen unterschiedlich „steil“. Bei Linearen Funktionen spricht man von der Steigung des Funktionsgraphen. Dieser wird bei uns mit dem Buchstabe „m“ abgekürzt.

Die Steigung lässt sich mit Hilfe eins sogenannten Steigungsdreiecks einzeichnen. Wie das geht wird dir im nachfolgenden Video kurz erklärt:

Übungsaufgabe zur Bestimmung der Steigung

Wie groß ist die Steigung m der nachfolgenden vier Funktionsgleichungen? Zeichne die Funktionsgraphen in ein Koordinatensystem (x- und y-Achse von -5 bis 5), ergänze passende Steigungsdreiecke. Lies anschließend die Steigung ab. Hinweis: f(x) ist eine alternative Schreibweise für y!

y = x
f(x) = -x
y = 0.5 x
f(x) = -3/2 x

y=x : Die Steigung beträgt 1 (Achtung, hier wird fälschlicherweise oft angenommen, dass die Steigung 0 beträgt)

f(x) = -x : Die Steigung beträgt -1

y = 0.5x : Die Steigung beträgt 0.5

f(x) = -3/2 x : Die Steigung beträgt -3/2 bzw. -1.5